8월 24일에 AIM Tech math quiz라는 게 열렸습니다. 수학을 좋아하는 저로서 참가를 안 할 수가 없기에, cs71107님과 팀을 이루어 참가했습니다. (팀 이름이 제 이름인 건 함정(?)입니다) 총 30문제였고, 대회는 2시간 동안 진행되었고, 스코어보드는 다음과 같습니다.
https://mathmaker.ru/contests/12eaac24-15d2-4d19-9afb-6e303ecba55e/2/standings
Math Platform
mathmaker.ru
30문제 중 24문제를 풀었고, 참가팀 35팀 중 7등을 했습니다. 그래도 대회 시간 동안 풀 만한 문제는 다 풀지 않았나 하는 생각은 듭니다. 문제들의 난이도는 5초 만에 풀 수 있는 문제부터, 아직도 완벽한 풀이를 모르는 문제까지 다양합니다. 업솔빙은 아래 링크에서 할 수 있습니다.
https://mathmaker.ru/contests/12eaac24-15d2-4d19-9afb-6e303ecba55e/3/1
Math Platform
mathmaker.ru
아래는 문제별 풀이입니다. 풀이에서 답을 안 써놓은 경우도 있는데, 답은 여기서 확인할 수 있습니다.
체감 난이도는 다음과 같습니다. 단순 계산이나 간단한 수학 지식에 익숙하신 분들은, 앞의 몇 문제는 건너뛰셔도 상관 없을 것 같습니다. 참고로 대회 때 저희 팀이 못 푼 문제는 19 20 21 27 28 30입니다.
1 2 3 4 5 6 8 9 10 / 7 11 12 13 14 15 16 17 18 / 22 23 26 / 24 25 27 29 / 19 20 21 28 30
1. What is the largest number which can be drawn using 15 matches?
번역: 15개의 성냥개비로 만들 수 있는 가장 큰 수는?

자릿수가 많으면 많을수록 좋을 것 같습니다. 그리고 큰 숫자가 앞에 있을수록 좋을 것 같습니다.
2. Find sum of the series \(\frac{1}{1 \cdot 4} + \frac{1}{2 \cdot 5} + \frac{1}{3 \cdot 6} + \frac{1}{4 \cdot 7} + \cdots \).
\(\frac{1}{n\cdot (n+3)} = \frac{1}{3}(\frac{1}{n} - \frac{1}{n+3})\)을 이용하면 될 것 같습니다.
3. The tractor began to plow the field, after some interval of time second tractor of the same kind joined it, then after the same interval - third, and so on until the last. It turned out that the first tractor worked five times longer than the last. If everyone had started at the same time, they would have done the work in 2 hours. How long had the first tractor actually worked?
번역: (동일한) 트랙터 3대가 일을 하는데, 첫 번째 트랙터가 일을 시작한 뒤, T분 뒤에 두 번째 트랙터가 일을 시작했고, 또 그 다음 T분 뒤에 세 번째 트랙터가 일을 시작했습니다. 일이 끝났을 때, 첫 번째 트랙터는 세 번째 트랙터보다 5배 더 일했습니다. 트랙터 3대가 동시에 일을 시작했다면 일은 2시간만에 끝났을 것입니다. 원래 상황에서 첫 번째 트랙터는 얼마나 일했을까요?
굳이 풀이를 쓰자면, 세 트랙터가 일한 시간을 5t, 3t, t라 놓으면 9t=120*3입니다.
4. The sum of infinite geometric series containing positive numbers is \(S\). The second term of the sequence is \(1\). Find the smallest possible value of \(S\).
번역: 양수만으로 이루어진 무한등비급수의 합이 \(S\)이고, 두 번째 항이 \(1\)입니다. \(S\)의 최솟값은?
수열의 공비를 \(r\)이라 놓으면 \(0<r<1\)이어야 합니다. 한편 초항은 \(\frac{1}{r}\)이므로 \(S=\frac{1}{r(1-r)}\)입니다. 이 값을 최소화하려면 분모를 최대화해야 합니다. 산술-기하 평균 부등식을 써도 되고, 이차함수의 최댓값을 구해도 됩니다.
5. Each of the 12 men is either a knight (always tells truth) or a liar (always tells lie). One of them said: "The number of liars among us is divisible by 1"; the second one said: "The number of liars among us is divisible by 2"; ...; the last one said: "The number of liars among us is divisible by 12". How many knights can be in this group?
번역: 12명의 사람이 있는데, 참말만 하는 참말쟁이거나 거짓말만 하는 거짓말쟁이입니다. 사람들에게 1부터 12의 번호를 매겼을 때, k번 사람은 "우리 중 거짓말쟁이의 수는 k의 배수야" 라고 말했습니다. 참말쟁이의 수로 가능한 값을 모두 구하세요.
거짓말쟁이의 수를 고정해놓고 나면, 누가 참말을 했는지가 정해집니다. 그렇게 정하고 나서 실제로 거짓말쟁이의 수가 고정해놨던 그 수인지를 확인하면 됩니다.
혹시 틀렸다면, edge case가 있지는 않을지 한 번 더 생각해봅시다.
6. An ant travels through the vertices of heptagon. Every second he moves to one of the two neighboring vertices with equal probability. Find probability that the ant will finish in the initial vertex after 9 moves.
번역: 개미가 7각형의 꼭짓점들을 돌아다니고 있습니다. 각 이동에서 개미는 이웃한 두 꼭짓점 중 랜덤으로 하나의 꼭짓점으로 갑니다. (양쪽 점으로 갈 확률은 0.5로 같습니다) 9번의 이동 이후 시작점으로 되돌아올 확률을 구하세요.
시작점으로 돌아오려면 8번 오른쪽, 1번 왼쪽으로 가거나, 1번 오른쪽, 8번 왼쪽으로 가야 합니다. 각각의 경우의 수는 9이고, 전체 경우의 수는 \(2^9=512\)입니다.
7. 20 teams participate in tournament. Every two teams play exactly one game between each other, winner receives 3 points, loser 0 points, in case of tie both teams receive 1 point. After the tournament all teams have been sorted by the number of points in descending order. What is the maximum possible point difference between two neighboring teams in such list?
번역: 20팀이 리그전에 참가합니다. 임의의 두 팀끼리는 정확히 한 번 맞붙고, 이기면 3점, 지면 0점, 비기면 1점입니다. 경기가 모두 끝나고 승점 순서대로 정렬했을 때, 이웃한 두 팀의 승점 차이로 가능한 값 중 최댓값은 얼마일까요?
가능한 최대 승점은 57점입니다. 이 때 나머지 팀들의 승점의 총합을 생각해보면, 경기마다 승점의 총합은 2 또는 3씩 늘어나므로, 최소 2 * (나머지 경기 수)는 됩니다. 이게 최대한 고르게 분배되어있을 때가 1등과 2등의 차이가 최대가 됩니다. 다른 등수 차이를 가장 큰 차이로 만들어보려 해도 이 때의 차이를 만들 수 없음을 확인할 수 있습니다.
8. Find the largest integer number \(n\) such that \(98!+99!+100!\) is divisible by \(5^n\).
번역: \(98!+99!+100!\)이 \(5^n\)의 배수인 최대의 \(n\)을 구하세요.
일단 식을 \(98!\)으로 묶으면 \(98!(1+99+100)\)이 됩니다. \(98!\)의 소인수분해에 5가 몇 번 나오는지 알 수 있다면 문제를 풀 수 있겠습니다.
9. Number \(m\) is chosen uniformly randomly from the set \(\{11,13,15,17,19\}\), and number \(n\) is chosen uniformly randomly from set \(\{1999,2000,\cdots,2017,2018\}\). What is the probability that the last digit of \(m^n\) is \(1\)?
번역: \(m\)은 집합 \(\{11,13,15,17,19\}\)에서 균일하게 랜덤으로 선택되며, \(n\)은 집합 \(\{1999,2000,\cdots,2017,2018\}\)에서 균일하게 랜덤으로 선택됩니다. \(m^n\)의 마지막 자리가 1일 확률은 얼마일까요?
10. For integer \(n\ge 2\), define \(f(n)\) as the largest integer \(m\) such that \(\sqrt[m]{n}\) is integer number. Find the value of sum \(f(2)+f(3)+\cdots + f(100)\).
\(k\)를 고정해놓고, \(f(x)=k\)인 \(x\)의 개수를 세면 편합니다. 제곱수라고 다 \(f(x)=2\)가 아닌 것만 조심하면 됩니다.
11. The number is called a palindrome if it is read the same in both directions (the number cannot start from 0). Vasya randomly uniformly chooses a 6-digit palindrome \(n\). What is the probability that the number \(\lfloor\frac{n}{11}\rfloor\) is also a palindrome?
대회 때는 그냥 코드 짜서 풀었습니다. 코딩 없이 풀자면, 어차피 개수만 세면 되고, 6자리 팰린드롬은 언제나 11의 배수니까, 5자리 팰린드롬 중에서 11을 곱해도 팰린드롬인 것의 개수를 세는 편이 생각하기 편합니다. 하다 보면 받아올림이 없으면 되는 것 같고, 받아올림이 없는 경우들만이 가능한 경우임을 알 수 있습니다. 개수를 셀 때는 가운데 수를 기준으로 세면 나름 규칙적으로 셀 수 있습니다. leading zero가 없어야 함은 언제나 주의하면 될 것 같습니다.
12. Tennis balls of radius 1 are packed in cylinder containers of radius 2 and height 1000. Find the maximum number of balls which can be packed in one container.
번역: 반지름이 2이고 높이가 1000인 원기둥에 반지름이 1인 공이 최대 몇 개 들어갈까요?
가로로 2개, 세로로 2개, 이런 모양이 반복됩니다. 이 때 두 층마다 중심들을 이은 도형은 정사면체가 됩니다. 정육면체의 이웃하지 않은 점 4개를 고르면 정사면체가 된다는 사실을 잘 생각해보면, 한 변의 길이가 2인 정사면체에서 마주보는 두 모서리의 거리는 \(sqrt{2}\)가 됨을 알 수 있습니다. \(sqrt{2}(x-1)+2 \le 1000\)을 풀면 층의 개수 \(x\)가 나옵니다.
13. Let \(\mathcal{P}\) be a parallelepiped (not necessarily rectangular) with sides \(x,y,z\). Let the 4 spatial diagonals \(\mathcal{P}\) have lengths \(15,17,21,23\). Find \(x^2+y^2+z^2\).
번역: 평행육면체의 세 변의 길이가 \(x,y,z\)이고, 면에 포함되지 않는 대각선 네 개의 길이가 각각 \(15,17,21,23\)입니다. \(x^2+y^2+z^2\)의 값을 구하세요.
평행육면체를 이루는 세 벡터를 \(v_1, v_2, v_3\)라 합니다. 이 때 각각의 대각선은 \(v_1 \pm v_2 \pm v_3\)로 나타낼 수 있습니다. 벡터의 길이의 제곱은 벡터 스스로를 내적한 값과 같으니까, 대각선 네 개의 길이의 합은 \((v_1+v_2+v_3)^2 + (v_1+v_2-v_3)^2 + (v_1-v_2+v_3)^2 + (v_1-v_2-v_3)^2 = 4(v_1^2+v_2^2+v_3^2)\)입니다.
14. Find the smallest 3-digit divisor of number \(10\cdots010\cdots01\). 0이 100개씩 있는 이 수의 약수인 세 자리 수 중 가장 작은 수를 구하세요.
15. At McDonald's, nuggets are sold in packs of \(9\) or \(20\). Find the maximum number \(n\) such that it is impossible to buy exactly \(n\) nuggets.
나름 유명한 문제인 데다가 closed-form formula가 있습니다. \(a,b\)가 서로소일 때 \(g(a,b)=ab-a-b\)입니다. 증명도 어렵지는 않으니 한 번 해 보는 것도 좋습니다. 참고로, 묶음의 단위가 3개 이상인 경우에 대해서는 일반적인 식은 알려져 있지 않습니다.
16. Consider function \(f(x) = \sum_{k=2}{10} (\lfloor kx \rfloor - k \lfloor x \rfloor)\), where \(\lfloor x \rfloor\) is the largest integer number which is not greater than \(x\). How many different values does the function \(f\) take for \(x \ge 0\)?
번역: 저 함수가 가질 수 있는 서로 다른 값의 개수는?
일단 \(x\)의 소수부만 중요합니다. \(x\)를 \(0\)에서 \(1\)까지 천천히 올린다고 생각하면, 값이 변하는 곳은 분모가 10 이하인 분수들임을 알 수 있습니다. 그러한 분수의 개수를 세면 되는데, 중복된 수는 한 번만 세야 하므로 기약분수를 셉니다. 오일러 \(phi\) 함수와 관련이 있는 것 같습니다.
17. Represent number 2020 as a fraction \(\frac{a_1!a_2!\cdots a_m!}{b_1!b_2!\cdots b_n!}\), where \(a_i, b_j\) are integer numbers, \(a_1>a_2>\cdots>a_m>0, b_1>b_2>\cdots>b_n>0\) and the value of \(a_1+b_1\) is the minimum possible. Find the value \(|a_1-b_1|\).
번역: 2020을 저런 형태의 식으로 나타내는데, \(a_1+b_1\)이 최소가 되도록 합니다. 이 때 \(|a_1-b_1|\)을 구하세요.
분자에 \(101\)이 소인수로 있어야 합니다. 그러므로 \(a_1\)은 최소 101입니다. 그러면 분모에 \(97\)이 소인수로 있어야 합니다. 그러므로 \(b_1\)은 최소 97이고, 남은 곱을 \(\frac{(n-1)!}{n!}\) 꼴로 잘 처리하면 이게 가능하다는 걸 확인할 수 있습니다.
18. Consider points in the plane \((x,y)\) with integer coordinates such that \(x^2+y^2=2^k\) where \(0 \le k \le 1000\) and one more point - \(0,0\). Find the number of squares having all vertices at these points.
일단 이 점들은 \((0,0), (0,2^k), (2^k,0), (2^k,2^k)\)뿐입니다. (증명의 흐름: 만약 \(k\)가 \(2\) 이상이면 \(x,y\) 모두가 짝수여야 하므로 양변을 \(4\)로 나누는 과정을 반복할 수 있고, 따라서 \(k=0, k=1\)의 base case만 남습니다.) 그리고 생기는 정사각형들이 매우 규칙적으로 나올 수밖에 없습니다.(증명... 하고 싶으신가요...?) 잘 세주면 되는데, \((0,0)\)을 중심으로 갖는 것들과, \((0,0)\)을 꼭짓점으로 갖는 것들을 나누어 세면 됩니다.
19. Rain has 3 eggs. One of them is rubber and can't crush. Unfortunately, Rain doesn't know which one. He is in a 100-storey skyscraper. If you throw a normal egg from the top floor, it'll break. How many times Rain should throw an egg to clearly identify the minimum floor from which an egg breaks?
The rubber egg can be thrown as many times as you like, the unbroken egg can be thrown again. An egg breaks if and only if it is thrown from the floor \(y\ge x\) where \(x\) is the number of the minimum such floor.
번역: 3개의 달걀이 있는데 하나는 가짜라 안 깨집니다. 가짜가 뭔지는 모릅니다. 100층짜리 빌딩에서 실험을 통해 계란이 깨지는 최초의 층 \(x\)을 알아내려 합니다. 100층에서 달걀이 깨진다는 사실은 알려져 있으며, 현재 층 \(y\)가 \(x\) 이상일 때에만 (정상) 계란은 깨집니다. 계란을 던지는 최소 횟수는 얼마일까요?
처음에 생각했던 아이디어는, 두 개씩 떨어뜨리면 깨지는지 아닌지를 확실히 알 수 있으니까, \(x_1, x_2, \cdots, x_k\)에서 달걀을 두 개씩 떨어뜨린다는 것이었습니다. 이 때 \(2x_1-1, 2(x_2-x_1)-1 + 2, 2(x_3-x_2)-1 + 4, \cdots, 2(x_k-x_{k-1})-1+2(k-1), 2k\)가 모두 어떤 값 이하면 됩니다. 이걸 \(2k\)로 잡느냐 \(2k+1\)로 잡느냐 두 가지를 해 보고 그 중 작은 값이 답이 아닐까 했는데 계산을 잘못해서 27을 냈습니다. 이렇게 했을 때 답은 28이고 대회 중에 답은 실제로 28이었습니다. 그런데 실제로는 (3개의 달걀을 잘 구분하고 있을 수 있다는 가정 하에) 더 좋은 방법이 있습니다. 한 층에 두 개씩 떨구는 게 좀 비효율적이니까, 그냥 \(x_1, x_2, \cdots, x_k\)에 하나씩 떨구되, 1번, 2번, 3번 달걀을 번갈아서 던지는 것입니다. 이 때 어떤 달걀이 \(x_i\)에서 깨졌다면, \(x_{i-1}\)에서 안 깨졌던 달걀은 \(x_{i-2}+1\)부터 \(x_{i-1}\)까지에서도 안 깨지는 게 당연하므로 굳이 다시 던질 필요가 없습니다. 그래서 \(x_{i-2}+1\)부터 \(x_{i-1}\)까지는 다른 달걀만 던지고, \(x_{i-1}+1\)부터 \(x_i-1\)까지는 두 달걀을 모두 던져보면 됩니다. 그래서 이 값이 \(k+1\) 이하가 되도록 잘 정해보면 되고, 그렇게 했을 때 \(x_k\)가 99 이상이 될 수 있다면 그 때의 \(k\)가 답이 됩니다. 시행착오를 통해 이 값이 23이라는 사실을 확인할 수 있습니다. 그 때의 최적의 \(x_i\) 수열은 다음과 같습니다.
\(12, 18, 26, 33, 40, 46, 52, 58, 63, 68, 73, 77, 81, 85, 88, 91, 94, 96, 98, 100, 101, 102, 103\)
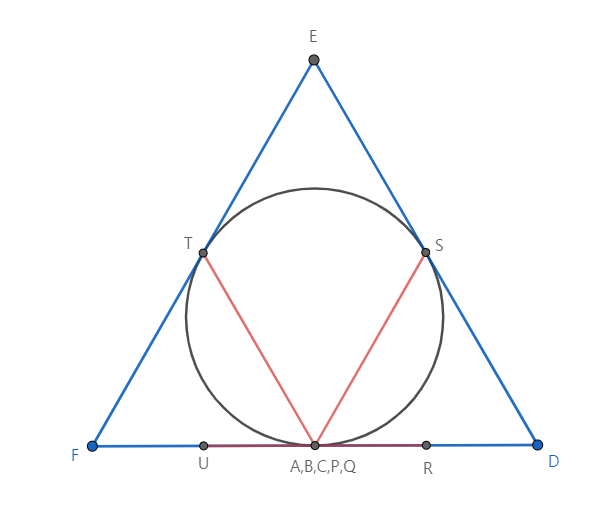
20. A convex hexagon is circumscribed around a circle of radius \(1\). Consider three line segments connecting the midpoints of opposite sides of the hexagon. For which largest \(r\) can we assert that at least one of these segments is at least \(r\)?
번역: 반지름이 1인 내접원을 가지는 육각형 ABCDEF이 있습니다. 마주보는 변(AB-DE, BC-EF, CD-FA)의 중점을 연결한 세 선분을 생각합니다. 세 선분 중 최소 하나는 \(r\) 이상임을 보장할 수 있는 최소의 \(r\)은 얼마일까요? (=세 선분 중 최대 길이의 하한은 얼마일까요?)
21. A jeweler made an open chain from \(2020\) consequently numbered rings. The capricious customer demanded to change the order of the rings in the chain. She ordered such an open chain so that the jeweler has to unlink as many rings as possible. How many rings does the jeweler have to unlink?
An unlinked ring can be disconnected from its neighbors in the chain and then linked together with other rings. For example, in the picture the unlinked are rings 2 and 5, and the chain on the left can be obtained by reversing the (3, 4) sub-chain and changing the order of other rings, while the chain to the right cannot be produced since in order to connect rings 1 and 3 one needs to unlink at least one of them, which is not the case.

번역: \(2020\)개의 고리가 \(1, 2, \cdots, 2020\) 순서로 일렬로 연결되어 있습니다. 어떤 고객이 이 chain의 순서를 특정 순서로 바꿀 것을 요구하였습니다. 고객이 요구한 대로 바꾸기 위해서는 고리를 몇 개 끊어야 합니다. 끊지 않은 고리는 다른 끊지 않은 고리와 연결할 수 없지만, 연결된 고리의 순서를 역순으로 바꾸는 것은 가능합니다. 그렇다면 각 배치마다 끊어야 하는 최소 고리의 개수가 나올텐데, 이 개수의 최댓값은 얼마일까요?
문제 이해가 쉽지 않습니다. 그림을 보고 대략 이해하면 되는데, 끊지 않은 고리끼리 연결할 수 없다는 게 핵심입니다. 일단 기본적으로 원래 배치에서 이웃했던 고리들이 절대 이웃하지 않도록 할 것입니다. 문제를 다음과 같이 접근합니다.
"보석 상인이 끊지 않을 고리를 정해갑니다. 이 때, 그 고리를 끊지 않도록 결정하게 되면서, 끊을 수밖에 없는 고리들이 생깁니다.(그 고리들은 원래 배치에서 그 고리와 이웃했던 고리들과, 나중 배치에서 그 고리와 이웃한 고리들입니다) 이것들을 제외하고, 다시 끊지 않을 고리를 정하고, 이 과정을 반복합니다."
이렇게 했을 때, 제외되는 고리의 개수는, 보석 상인이 최선을 다한다면 (끊지 않기로 선택한 고리 포함) 최대 4개입니다. 즉 4개를 제외할 때마다 최소 하나는 안 끊는다는 것입니다. 어떻게 최선을 다하는지는, 이미 제외하기로 결정된 고리와 이웃한 고리 or 양 끝에 있는 고리를 고르면 됩니다. 한편, 고객이 최선을 다하면, 어떻게 고리를 선택하더라도 4개 이상 지워지도록 할 수 있습니다. (1-2-3-4) -> (3-1-4-2)는 어떤 고리를 끊지 않기로 결정하는 순간 다른 모든 고리를 끊어야 하는 배치입니다. 이걸 반복하면 됩니다. (1-2-3-4-5-6-7-8) -> (3-1-4-2-7-5-8-6)과 같이 말이죠. 답은 뭘까요? 4개마다 3개를 지워야 하니까 \(2020\cdot 3/4\)겠군요.
22. Consider permutations of integer numbers from \(1\) to \(10^9\). Denote the number of odd permutations without fixed points by \(O\), and the number of even permutations without fixed points by \(E\). Find the value of \(E-O\).
번역: \(1\)부터 \(10^9\)의 순열을 생각합니다. 홀순열인 교란순열의 개수를 \(O\), 짝순열인 교란순열의 개수를 \(E\)라 할 때, \(E-O\)를 구하세요.
교란순열: 모든 \(i\)에 대해 \(i\)번 위치가 \(i\)가 아닌 순열
홀순열, 짝순열: 순열을 항등 순열(\(1, 2, \cdots, n\) 순서로 된 순열)로 만들기 위한 교환 횟수는 어떻게 교환하더라도 홀짝성이 변하지 않는데, 그 교환 횟수가 홀수면 홀순열, 짝수면 짝순열입니다.
순열에서 교환을 한 번 할 때마다 홀짝성이 바뀜에 주목합니다. \(1\)부터 \(n\)까지의 순열에 대해 \(E-O\)의 값을 \(x_n\)이라 합니다. \(n\ge 3\)일 때, 각 교란순열에 대해 \(1\)과 \(2\)의 위치를 바꿉니다. 바꾼 것도 교란순열인 경우, 둘 중 하나는 홀순열, 다른 하나는 짝순열이므로 \(x_n\)을 계산할 때 상쇄됩니다. 바꾼 것이 교란순열이 아닌 경우가 있는데, \(1\)번 위치가 \(1\)이어서 그럴 수도 있고, \(2\)번 위치가 \(2\)가 아니어서일 수도 있고, 둘 다일 수도 있습니다. \(1\)번 위치는 \(1\)이고 \(2\)번 위치는 \(2\)가 아닌 경우, \(1\)을 제외한 나머지가 교란순열입니다. 여기서 \(E-O\)가 \(x_{n-1}\)이니까, 원래에서 \(E-O\)는 (한 번 바꿨으므로) 부호가 바뀌어 \(-x_{n-1}\)만큼 기여합니다. 마찬가지로 나머지 경우에서 각각 \(-x_{n-1}, -x_{n-2}\)의 기여를 받으므로, 최종적으로 \(x_n=-2x_{n-1}-x_{n-2}\)입니다. 그리고 \(x_1=0, x_2=-1\)입니다. 이 점화식을 풀면(실제 대회 때는 팀원이 규칙을 찾아서 일반항을 구했습니다만) \(x_n=(-1)^{n-1} \cdot(n-1)\)입니다.
23. Sequence \(\{a_n\}\) is defined by the following recurrent rule: \(a_0=1, a_1=\sqrt[19]{2}, a_n = a_{n-1}^2 a_{n-2}\) for all \(n \ge 2\). Find the smallest integer \(k\) such that \(a_1a_2\cdots a_k\) is integer number.
24. There are exactly \(77000\) quadruples \(a,b,c,d\) such that \(gcd(a,b,c,d)=77\) and \(lcm(a,b,c,d)=n\). What is the minimum possible value of \(n\)?
뭔가 소인수분해를 해서 각 소인수를 잘 분배해야 할 것 같습니다. 지수가 \(k\)일 때 경우의 수가 \(12k^2+2\)가 나옵니다. 이 값들을 잘 모아보면 \(14, 50, 110, 194, 302, \cdots\)인데, 앞의 세 개를 곱하면 \(77000\)이 됩니다. 그래서 답은 \(77\cdot 2^3 \cdot 3^2 \cdot 5\)입니다.
25. Consider parking for 2020 cars. All spots are situated along the line and are numbered from 1 to 2020. Arriving cars park as follows: the first car chooses the place uniformly randomly. Each next car selects the place from which the distance to the nearest car will be the greatest (one of such places with equal probability). Find the probability that the last (2020-th) car will occupy parking spot with number 1.
번역: 2020대의 차가 주차를 하는데, 첫 번째 차는 아무 데다 대고, 그 다음 차부터는 가장 가까운 차와의 거리가 최대가 되도록 하는 위치 중 하나를 랜덤으로 골라서 댑니다. (모든 랜덤은 uniform) 마지막 차가 1번 위치에 댈 확률은?
첫 차가 어디에 대느냐가 많이 중요합니다. 1011~2020에 대면 그 다음에 대는 곳이 바로 1번이 되니까 안 되는데, 앞쪽에 대도 생각보다 문제가 됩니다. 심지어는 3번에 대더라도, 2번보다는 1번을 무조건 먼저 대게 되어 있어서 마지막 위치가 1번이 될 수가 없습니다. 결국 첫 차가 2번에 대야만 한다는 결론이 나옵니다. 그 다음은 약간의 노가다인데, 가장 가까운 거리가 1이 되기 전까지 차를 열심히 댑니다. 그러면 자리가 몇 개 남을까요? 1번을 제외하고 1024개가 남습니다. (1024가 뭔가 매우 익숙한 수라는 생각이 들었을 수도 있는데, 조금 놀랍게도(?) 어떤 수에서 시작해도 2의 거듭제곱으로 끝납니다!) 이제 1025개 중에서 1번이 제일 마지막일 확률은 1/1025입니다. 이 확률을 첫 차가 2번에 댈 확률 1/2020과 곱해주면 됩니다.
26. Lets denote the distance between 5-digit numbers \(\overline{a_1a_2a_3a_4a_5}\) and \(\overline{b_1b_2b_3b_4b_5}\) as the largest \(i\), for which \(a_i\neq b_i\). All 5-digit numbers are written down in some order. What is the smallest possible sum of distances between adjacent numbers?
뒤집은 수가 작은 것부터 큰 순서대로 놓으면 됩니다. 이 때가 최솟값이라는 것은, \(a_5\)는 최소 9번 변해야 한다는 사실, 그리고 각 \(a_5\)가 같은 구간마다 \(a_4\)가 9번씩은 변해야 한다는 사실 등등을 종합해보면 알 수 있습니다.
27. Find the maximum size of the square, which can be placed inside the cube with edge of length 1.
삼수선의 정리 같은 걸 생각하다 보면, 정사각형을 어떤 한 면에 정사영시켜 직사각형을 만들었을 때, 그 직사각형이 정사각형 안에 들어가면 된다는 사실을 알 수 있습니다. 이 직사각형의 이웃한 두 변의 길이는 각각 \(b, \sqrt{1+b^2}\)이 되며, 가능한 \(b\)의 최댓값은 \(\frac{\sqrt{2}}{4}\)입니다. 이 때 원래 정사각형의 한 변의 길이는 \(\frac{3\sqrt{2}}{4}\)입니다.
28. Each of the 2020 cards has a number written on it, all these 2020 numbers are different. The cards are turned upside down. In one move, it is allowed choose ten cards, and in response, one of the numbers written on them will be reported (it is not known which one). What is the largest \(t\), such that it is guaranteed to be able to find \(t\) cards, about which it is known what number is written on each of them?
번역: 2020장의 카드가 있습니다. 각 카드에 쓰여 있는 수는 모두 다릅니다. 10장의 카드를 고르면 judge는 그 중 하나의 카드에 쓰여 있는 수를 알려줍니다. (어느 카드인지는 모릅니다) 최악의 상황에서도 \(t\)장의 카드에 쓰여 있는 수를 정확하게 알 수 있다 할 때 \(t\)는 최대 얼마일까요?
참가자의 입장에서는 몇 번을 물어봐도 되니까 가능한 모든 조합을 물어봅니다. judge의 입장에서는 정보를 많이 줄수록 불리하므로 각 조합에 대해 무조건 정해진 수를 알려줍니다. judge의 입장에서 생각하면 몇 개까지의 수를 숨길 수 있느냐 하는 문제가 됩니다. 그런데 숨기는 수들 중에서만 10개를 골랐을 때도 judge는 답변을 해야 하기 때문에, 결국 어떤 수가 어느 위치에 있는지를 완전히 숨길 수 있는 \(n\)의 최댓값을 구하면 됩니다. 좀 많이 어려운데, 비둘기집을 만든다고 생각합니다. 조금 작은 경우를 보면, 2개의 카드를 고르는 상황을 생각하면 \(n=3\)일 때는 숨길 수 있습니다. \((1,2):x_1,(2,3):x_2,(3,1):x_3\) 이렇게 주면 참가자는 \((x_1, x_2, x_3)\)와 \((x_3, x_1, x_2)\)의 상황을 구분할 수 없습니다. \(n=4\)일 때는 숨길 수 없음을 확인할 수 있습니다. 이제 10개를 고르는 상황에서는, 저런 삼각형 고리를 9개 만들어 놓으면, 10개를 고르면 비둘기집 원리에 의해 어떤 고리에서는 2개를 고르게 되어 있습니다. 그 고리 내에서의 규칙에 따라 수를 공개합니다. 이렇게 하면 27개를 완전히 숨길 수 있고, 수학적 귀납법으로 이 값이 최대임도 증명할 수 있습니다. 구하려는 답은 \(2020-27\)입니다.
29. Let \(a, b, c, d\) be positive real numbers which satisfy the following system of equations
\((a+b)(c+d)=143, (a+c)(b+d)=150, (a+d)(b+c)=169\).
Find the minimum possible value of \(a^2+b^2+c^2+d^2\).
\(a+b+c+d=t\)라고 놓습니다. 그러면 \((a+b)\)와 \((c+d)\)는 합이 \(t\)이고 곱이 \(143\)인 두 수입니다. 그러므로 \((a+b)^2+(c+d)^2=t^2-286\)입니다. 마찬가지로 \((a+c)^2+(b+d)^2=t^2-300, (a+d)^2+(b+c)^2=t^2-338\)입니다. 세 식을 다 더하면 좌변에 \((a+b+c+d)^2=t^2\)으로 소거할 수 있는 형태가 하나 생기고, 정리하면 \(a^2+b^2+c^2+d^2=t^2-462\)입니다. 가능한 \(t\)의 범위는, 판별식들(\(t^2-169\cdot 4 \ge 0\)) 등등으로부터 나옵니다. 그렇게 구한 \(t\)의 최솟값을 넣으면 구하려는 최솟값이 나옵니다.
30. Find the determinant of the following matrix
\(\left(\binom{7i+5j}{j}\right)_{0\le i,j \le n}\).
j열이 i에 대한 j차식이 된다는 걸 알 수 있습니다. elementary row operation을 반복하다 보면, 결국 이걸 최고차항만 남길 수 있다는 사실을 알 수 있습니다. \(\left(\begin{smallmatrix}1 & 1 & 1\\7\cdot 1 & 7\cdot 2 & 7\cdot 3\\\frac{7^2}{2}\cdot 1^2 & \frac{7^2}{2}\cdot 2^2 & \frac{7^2}{2}\cdot 3^2\end{smallmatrix}\right)\) 이런 식으로 말이죠. 앞에 \(7^k\)들을 밖으로 빼고 다시 이항 계수 형태로 바꿔주면 Pascal matrix가 됩니다. (Symmetric form) 이 행렬의 determinant는 1입니다. 그러므로 구하려는 답이 \(7^{\frac{n(n+1)}{2}}\)라는 사실을 알 수 있습니다.
'수학' 카테고리의 다른 글
| 루트 2가 무리수임을 n가지 방법으로 증명해보기 (1) | 2019.07.01 |
|---|